The High Instantaneous Current Spec

This very subject came up recently in the Audioholics forum and I would like to expand on this subject further, but before I do I think it's important to go into the history of how this specification became popular.

A Brief History

In the early days of stereo and stereo loudspeaker design some loudspeaker designers did not pay close attention to the impedance of the crossover in the loudspeaker. This resulted in some very low impedances at certain point(s) in the crossover, and the power amplifier would be required to "dump" excessive amounts of current to meet the demand. This practice pretty much fell out of favor by the early 1990's as speaker designers decided that this was not very good design and it also forced users to have huge, heavy, and excessively powerful amplifiers. A majority of the better Home Theater loudspeaker designers have decided, for the better I might add, not to repeat these mistakes.

The High Instantaneous Current test was typically a short burst of either a sine or square wave into a very low resistive load. The amount of current was derived by observing how much voltage could be developed across the load before it clipped, blew a fuse, or in some cases just blew up.

Many manufacturers decided to "enhance" their designs at the time to meet this spec but with great sacrifices in other areas. Typically a manufacturer would use a higher voltage rated transformer but lower steady state current to put a higher potential across the main power supply capacitors giving higher values of instantaneous current. The problem with this was that during moderate sustained energy plateaus the transformer would saturate and radiate excessive amounts of magnetic field, draw excessive current from the AC line and radiate more heat. This gave birth to some of the worst in power supply design in audio history. The staff at Audioholics will soon be monitoring amplifiers under test for this type of poor power supply design and reviews will include monitoring of the AC line with the unit under various load conditions.

There is also an important lesson for audiophiles and HT people here. Typically a manufacturer will give a VA rating for the transformer in a given unit. Note that the VA rating does not give you how many volts and how many amps for the transformer, it gives the combination of the two. For example: If I have a 400VA transformer I could have a transformer that is rated at 40 volts and 10 amps or I could have a transformer rated at 80 volts and 5 amps. The VA rating is the same for both!

The Application

Does this test really apply to either Home Theater or Stereo Loudspeakers in use today and even in the past decade? Lets look for a minute or so at some basic math that will help understand as it applies to amplifiers and loudspeakers. For the entire example I will use 75 amps of current which was the figure bandied about in the Audioholics forums.

How Do We Define Power?

Power is a function of three but very interrelated variables. They are as follows:

• Voltage
• Current
• Resistance/Impedance
  
  

The Basic power formulas are as follows:

• Power (watts) = Voltage (volts) times the current (amps)
• Power (watts) = the square of the voltage (volts) divided by the resistance/Impedance (ohms)
• Power (watts) = the square of the current (amps) times the resistance/impedance (ohms)

Now that we are armed with our basic mathematical formulas lets take a look at what happens into actual loads.

For an 8 ohm load with 75 amps:

• Power (watts) = the square of the current (amps) times the resistance/impedance (ohms)
• Power = 75 amps times 75 amps times 8 ohms which = 45,000 Watts!

However, we need a voltage across that 8 ohms to produce that 45,000 watts so to find that voltage we use this next formula.

• Power (watts) = Voltage (volts) times the current (amps) or Algebraically this formula converts to:
• Voltage (volts) = Power (watts) divided by the current (amps)
• Voltage = 45,000 divided by 75 which equals 600 volts!

But Wait a Minute Here: No audio amplifier has power supply rails to that go to 600 volts, the maximum we might find for some of the largest sound reinforcement amplifiers used for live concerts is somewhere between 80 to 95 volts, which a far cry from 600 volts. So we can conclude that our high instantaneous current into 8 ohms is just not useable.

Let's try cutting our load in half which brings us to 4 ohms.

• Power (watts) = the square of the current (amps) times the resistance/impedance (ohms)
• Power (watts) = 75 amps times 75 amps times 4 ohms.
• Power = 22,500 watts!

To find the voltage across the 4 ohm load to produce this power we need the following formula:

• Power (watts) = Voltage (volts) times the current (amps) or Algebraically this formula converts to:
• Voltage (volts) = Power (watts) divided by the current (amps)
• Voltage (volts) = 22,500 divided by 75 amps which equals 300 volts!

AGAIN this is approximately three times higher than our supply rails for even the largest amplifiers. So once again we can conclude that our high instantaneous current into 4 ohms is just not useable.

Let's cut our load in half once again to 2 ohms and let's see what we find.

• Power (watts) = the square of the current (amps) times the resistance/impedance (ohms)
• Power (watts) = 75 amps times 75 amps times 2 ohms.
• Power = 11,250 watts!

To find the voltage across the 2 ohm load to produce this power we need the following formula:

• Power (watts) = Voltage (volts) times the current (amps) or Algebraically this formula converts to:
• Voltage (volts) = Power (watts) divided by the current (amps)
• Voltage (volts) = 11,250 watts divided by 75 amps, which equals 150 volts!

YET AGAIN this is just over 50 volts higher than our power supply rails for even the largest amplifiers. So once again we can conclude out high instantaneous current into 2 ohms is not useable.

Let's try cutting our load to 1 ohm and see what happens.

• Power (watts) = the square of the current (amps) times the resistance/impedance (ohms)
• Power (watts) = 75 amps times 75 amps times 1 ohms.
• Power = 5,625 watts!

Power (watts) = Voltage (volts) times the current (amps) or Algebraically this formula converts to:

• Voltage (volts) = Power (watts) divided by the current (amps)
• Voltage = 75 volts

We now are starting to get close to out largest power supply rails but there is one major problem here:

Loudspeakers Used for Home Theater Don't Go Down to One Ohm!!!

I think the only loudspeaker today that goes down close to one ohm are some of the Martin Logan Electrostatic Loudspeakers and that is only at frequencies above approximately 15 kHz. Since this end of the spectrum is only harmonic content, only a few watts are needed here. Below about 8 kHz the speaker is a relatively benign 4 ohm load.

Power Table Summary for Various Loads under the 75A Current Specification

The High Instantaneous Current Spec - page 2

The Reactive Load

Marketing specialists over the years have claimed that "high current" is needed to drive a loudspeaker due to the reactive load that loudspeaker represents to the amplifier. But is this true? Let's take a closer look at this.

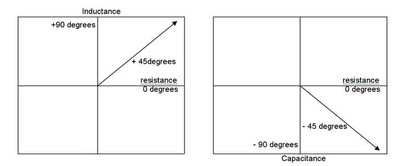
If we take a look at a typical loudspeaker impedance curve we find that the impedance will vary from +/- 30 degrees to +/- 45 degrees. We know that a 45 degree phase angle is half way between 0 degrees and 90 degrees.

Note the diagrams below:

Note that when the phase angle is + 45 degrees half of our load is inductive and half is resistive. Also note that when our phase angle is - 45 degrees half of our load is capacitive and half is resistive. The resultant of this combination that gives an impedance and that impedance is also measured in ohms.

So will high current help us drive the reactive load? The answer is NO because all the formulas in the previous section still apply. The only time there is a problem is when the reactive load goes very close to either +/- 90 degrees, but since that never happens in a loudspeaker this is not an issue.

In reality there will be less power to the load and this is due to Power Factor. Power Factor states that whenever you have a reactive load the voltage and current are out of phase with each other and the degree of the phase angle tells us how much power is lost. The key here is to remember that maximum power is only applied to a pure resistive load, and that power diminishes as the phase angle of a reactive load becomes greater and greater.

In the past a company named Apogee made ribbon loudspeakers that were very inefficient and some of them had an impedance that went down to about 1.5 ohms. Looking at the impedance plots for these speakers showed the phase angle was pretty small but the resistance was very low. These loudspeakers were the exception, they are not the rule, and they aren't made anymore.

Conclusion

From the math and what we know about the basics of how amplifier and loudspeakers perform we can now conclude that High Instantaneous Current is a non-issue and it has no application to driving contemporary and even most of the not so contemporary loudspeakers. In the past, a number of so-called simulations of what music is supposed to represent have been tried to more accurately gauge amplifier power. They have all been dismal failures due to the nature of classical/symphonic music, which has a stunning ability to throw a wrench into just about any generalization. Since many soundtracks use symphonic music this is just as important to Home Theater enthusiasts as well as classical music lovers.

It is the authors firm conviction and experience in designing, building and selling amplifiers that the watts rms into a given load, (8 ohms, 4 ohms, 2 ohms, etc., etc.) over the audio bandwidth of 20 Hz to 20 kHz, is the only accurate and representative way to measure power for this application. For those of you who prefer peak power measurements just remember this: If we multiply the watts rms figure times two we get peak power. So yes, the good old watts rms measurement is also a measure of peak watts.

Special thanks to Dan Banquer of www.redesignsaudio.com

This article was originally published June 5th, 2005.  We are republishing in the memory of Dan Banquer who passed away at the age of 58 years old last Saturday (October 15th, 2011). Dan was a dear friend of ours who was a no nonsense guy and true Audioholic in mind and spirit.  He will be missed by many...