Human Hearing - Phase Distortion Audibility Part 2

Given all the foregoing research presented in various academic, scientific & industry journals, as well as other media, variously indicating the audibility of phase distortion, there remains no valid doubts regarding the existence of phase distortion.

See for yourself: pass an audio signal through, for example, a 4th order LR crossover network and view the output on an oscilloscope and the waveform will appear to be a grossly distorted copy of the original.

Pass the same output signal through a spectrum analyzer and the amplitude of the various components will be correct, but their relative phase will have changed. Given the ready availability of software-based spectrum analyzer software and signal generators, investigation of this phenomenon is today almost a trivial exercise in signal analysis.

With these tools, it's certainly easy to visually assess phase distortion, but how easy is it to aurally assess this form of phase distortion? Let's take a look at a few examples of results & opinions arising from some commonly-cited research efforts.

In "On the Audibility of Midrange Phase Distortion in Audio Systems" by Lipshitz, et. al. we have:

" 1) Even quite small midrange phase nonlinearities can be audible on suitably chosen signals.

2) Audibility is far greater on headphones than on loudspeakers.

3) Simple acoustic signals generated anechoically display clear phase audibility on headphones.

4) On normal music or speech signals phase distortion appears not to be generally audible, although it was heard with 99% confidence on some recorded vocal material."

Lipshitz. et .al. used 1st & 2nd order unity-gain all-pass networks with f0s of ~ 100 Hz to 3kHz,

switchable in increments. For the 2nd order networks Q ranged from .5 to 2  in  increments. Some highlights of their experiments and results were:

Item

• Using 150 Hz square waves, pitch & timbre changes were notable for all Q and fo's. Though the effect was audible down to ~ 60 db SPL, it was most noticeable at higher dB SPL's.
• Using 2 - 5 Hz repetition rate square waves audible phase effects were again noted, this time as a ringing of the networks at fo. This effect was most noticeable with high network Q settings and across the 113Hz to 529 Hz frequency range, with detection becoming more difficult above 1 kHz.
• Using a raised-cosine tone burst, audible signal changes in the 160 Hz to the 353 Hz range fed through a 2nd order all-pass network, with Q's 1. When the same tone bursts were fed through Low-Q, 1st order networks, the audible signal changes were that occurred were of a much lower magnitude.
• Using pre-recorded music (male & female singing) fed through a 2nd-order all-pass network, with a Q of .5, audible effects were noted with a 95% confidence level. Using a variety of unpitched sounds recorded anechoically, phase effects were again audible.

And from Dr Floyd Toole:

" It turns out that, within very generous tolerances, humans are insensitive to phase shifts. Under carefully contrived circumstances, special signals auditioned in anechoic conditions, or through headphones, people have heard slight differences. However, even these limited results have failed to provide clear evidence of a 'preference' for a lack of phase shift. When auditioned in real rooms, these differences disappear.. ."

Essentially, Dr Toole expressing the opinion he does here (based on decades of his own,

often groundbreaking research), captures the essence of the conclusions reached by Lipshitz et. al.

In Daisuke Koya's "Aural Phase Distortion Detection":

" Although not in large numbers, previous research in investigation of the audibility of phase distortion has proven that it is an audible phenomenon. Lipshitz et al. has shown that on suitably chosen signals, even small midrange phase distortion can be clearly audible. Mathes and Miller and Craig and Jeffres showed that a simple two-component tone, consisting of a fundamental and second harmonic, changed in timbre as the phase of the second harmonic was varied relative to the fundamental. The above experiment was replicated by Lipshitz et al., with summed 200 and 400 Hz frequencies, presented double blind via loudspeakers resulting in a 100% accuracy score.

An experiment involving polarity inversion of both loudspeaker channels resulted in an audibility confidence rating in excess of 99% with the two-component tone, although the effect was very subtle on music and speech. Cabot et al. tested the audibility of phase shifts in two component octave complexes with fundamental and third-harmonic signals via headphones. The experiment demonstrated that phase shifts of harmonic complexes were detectable.

Another very simple experiment conducted by Lipshitz et al. was to demonstrate that the inner ear responds asymmetrically. Reversing the polarity of only one channel of a pair of headphones markedly produces an audible and oppressive effect on both monaural and stereophonic material. This effect predominantly affects frequency components below 1 kHz.

Because reversal of polarity does not introduce dispersive or time-delay effects into the signal, but merely reverses compressions into rarefactions and vice versa, these audible effects are due only to the constant 180° phase shift that polarity reversal brings about.

Since interaural cross-correlations do not occur before the olivary complexes to which the acoustic nerve bundles connect, it must be concluded that what is changed is the acoustic nerve output from the cochlea due to polarity reversal. This change owes to two factors: cochlear response to the opposite polarity half of the waveform, and the waveform having a shifted time relationship relative to the signal heard by the other ear. This reaffirms the half-wave rectifying nature of the inner ear. "

A frequent argument to justify why phase distortion is insignificant for material recorded and/or reproduced in a reverberant environment is that reflections cause gross, position-sensitive phase distortion themselves. Although this is true, it is also true that the first-arrival direct sound is not subject to these distortions, and directional and other analyses are determined during the first few milliseconds after its arrival, before the pre-dominant reverberation's arrival. Lipshitz et al. do not believe that the reverberation effects render phase linearity irrelevant, and there exists confirmatory evidence."

Let's take a closer look at Daisuke's test and results.

The test signals employed were:

• 70 Hz sawtooth wave
• 3.5 kHz sawtooth wave
• 10 kHz sawtooth wave
• Impulse
• Jazz-vocal group
• Percussion instruments.

A Kwalwasser - Dykema based test model was employed by the researchers. In this particular implementation, the test subjects were presented with two signals, one all - pass filtered, the other not. The test subjects (15 in all) then had to indicate whether or not a difference was heard. The 6 - signal test run was done using first headphones, then loudspeakers.

First, the headphone-series results:

Here, τmax is peak group delay for the particular filter used, msec

And the results for the loudspeaker run:

Comparing the results encapsulated in both tables it would appear we can reasonably draw the following conclusions:

• The number of correct responses given for the loudspeaker-based test is lower for just about every test signal used when compared to those reported in the headphone run.
• The results from the loudspeaker run appear more independent of the level of phase distortion present than that presented by the headphone run.
• The audibility of phase distortion in steady state signals was frequency dependent for both
• the loudspeaker and headphone runs.

Research work done in a controlled, scientific manner is a good first step in sorting fact from fiction - this holds true whether the study's subject matter is subjective or objective in nature.

An essential second step is the correct application of statistical analysis to the results. Oftentimes, the raw data that are the study's results present an impression or picture that can easily lead to false or otherwise incomplete interpretation. From that, incorrect conclusions can easily be drawn. Quality research simply requires the application of statistical analysis in order for the results to be correctly interpreted.

Now have a look at the next table, which outlines the correct number of responses, r, needed to conclude that the performance in each trial was better than that obtained by simple chance.

For this experiment in the audibility of phase distortion, the researchers chose r ≥ 9 as that point where r represents a statistically significant result.

Applying the r ≥ 9 requirement to classify a result as statistically significant, we can now view the data presented in the two tables in a very different light.

When applying the r ≥ 9 requirement, none of the 12 trials run in the loudspeaker series indicated a statistically significant result, though the Impulse test signal @ 4 m Sec comes very close at r = 8.5 . Only 4 of the 12 headphone trials indicated a statistically provable presence of the audibility of phase distortion.

So what useful information can we draw from this particular study?

• Phase distortion is audible, but only under very specific circumstances, using very specific, types of test signals.
• There exists in this study no statistically significant evidence supporting the audibility of phase distortion in the musical samples provided, using the all-pass filter implementations chosen by the researchers.
• Introducing the room acoustic variable in to the equation further lowers the already poor scores phase distortion audibility scores.

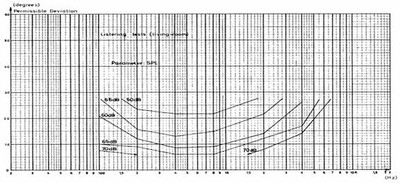
One other study I'd like to cite was that done by V. Hansen and E. R. Madsen. Originally published in the Journal of the Audio Engineering Society, in a 2-part series of articles.

They presented their test subjects a series of test tones, from the resulting data they were then able to determine permissible phase deviation levels for a variety of dB SPL levels. Of particular interest is how the presence of the positive slopes at the upper frequency portions of the curves support item 3 mentioned above in the first set of Daisuke study conclusions. These are given in Graphic 3.

So what conclusions regarding the audibility of phase distortion can we draw from the all of the above?

• Given the data provided by the above cited references we can conclude that phase distortion is indeed audible, though generally speaking, only very subtly so and only under certain specific test conditions and perception circumstances.
• The degree of subtly depends upon the nature of the test signal, the dB SPL level at which the signal is perceived, the acoustic environment in which the signal was recorded and/or played back as well as the Q & fo of any filter networks in the signal stream. Certain combinations of conditions can render it utterly inaudible.
• Room acoustics further masks whatever cues that the hearing process may depend upon to detect the presence of phase distortion.

Feedback from Dr. Floyd Toole (Added 4/08/05)

Thanks for bringing these articles to my attention. I guess the only comments I might have added relate to the differences in the perceptual tasks in the various studies leading to minimum audible amplitude shifts. Some were basically broadband or single tone, turn the volume up, kinds of tests. These 'difference limen, or just-noticeable difference' for loudness tests are fundamentally different from the ones that Sean Olive and I did, which was a just-noticeble timbre difference test - only a portion of the total sound spectrum was altered. Somewhere in the recesses of auditory signal processing they are probably related, but they are very different at a higher perceptual level. In any event, it is interesting to see anyone discussing the topic.

As was mentioned, our sensitivity to the timbral changes was very much dependent on the Q, or bandwidth of the phenomenon - with much lower 'thresholds' being found for wider bandwidth spectral changes. Interesting, because the narrower the bandwidth, the more the resonant system rings. Except, perhaps, at very low frequencies, it seems that we do not exhibit a primary response to the time-domain (ringing) problems but instead to the spectral features. Our sensitivity to resonances was also dependent on program material - pink noise was the most revealing, big band/symphonic with reverb was next, and the least revealing was close-miked pan-potted pop and jazz. Reverberation alone could increase our sensitivity to a medium or low-Q resonance by about 10 dB - a huge effect. This latter fact explains why music is so much more satisfying in a reverberant space than outdoors - timbrally richer because we can hear more of the resonant subtleties. It also explains why the toughest test for loudspeaker accuracy is in a room with some reflections, and why headphones (which have no added reflections) have an inherent advantage, and can sound acceptable when measurements indicate that there really are resonant problems. Killing all early reflections with absorbers not only changes imaging, it also makes loudspeakers with poorly controlled directivity sound better. All interesting stuff for audio folk.

The piece on phase distortion was a refreshing change from the semi-science floating around our business. All things being equal, and if one has the option, of course get the phase correct - at least at the one point in space where it can be done!! However, this presents problems for two-eared listeners in multiple seats in reflective rooms (solve this one and a Nobel prize awaits). It is indeed fortunate that humans are so unresponsive to this effect because, if we could hear phase shift, we would go absolutely nuts in everyday life. Every time a reflected version of a sound adds to the direct sound, the phase shifts are enormous, and it happens in abundance in all rooms, even carrying on a conversation across a table. Do the stand up/ sit down test while speaking. The voice changes very subtly, but our hearing system compensates immediately and, on a scale of 10, the voice quality remains a 10. Yet the transfer function between the voice and the ears has greatly changed in both amplitude and phase. I cannot help but think of all the opera recordings and film voice overs that are done with librettos and scripts on large angled (sound reflecting) surfaces between the mouth and the mic. The signal is corrupted at the source! Thank your favorite diety for human adaptability.

Keep up the good work.

Floyd

Floyd E. Toole, PhD
Vice President Acoustical Engineering
Harman International Industries, Inc.

Bibliography

Koya, Daisuke: " Aural Phase Distortion Detection", Masters dissertation,

Master of Science in Music Engineering Technology,

University of Miami , Coral Gables , Fla. , May 2000

Hansen, V and Madsen, E. R.: "On Aural Phase Detection " (J. Audio Eng.

Soc., vol. 22, pp. 10-14 (1974 Jan./Feb.))

Hansen, V and Madsen, E. R.: "On Aural Phase Detection: Part II,"

(J. Audio Eng. Soc., vol. 22, pp. 783-788 (1974 Dec.))

Lipshitz, S. P., Pocock, M., and Vanderkooy, J., "On the Audibility of Midrange Phase

Distortion in Audio Systems," J. Audio Eng. Soc., vol. 30,

pp. 580-595 (1982 Sep.).

Green, Steve: "A New Perspective on Decimation and Interpolation Filters ,

Cirrus Logic, Inc., July 2004

Walker, R.: "Acoustic Modeling - approximations to the real world",

BBC R & D White Paper WHP 005, London , Eng. , September 2001

Gerzon, Michael: "Why do equalizers sound different?", Studio Sound, July 1990

Cabot, Richard C., " Audible Effects vs. Objective Measurements In The

Electrical Signal Path", Audio Engineering Society,

8th International Conference

Linkwitz, S.: " Group delay and transient response "